Τα παράξενα της ρίζας του 2!

<===============>

Ρίζα του δύο;;!! Θα πει ο άλλος! Ξέρω, κακές αναμνήσεις από τα μαθηματικά! Τη ρίζα του δύο την πρωτοσυναντήσαμε στο γυμνάσιο. Αλλά δεν σκοπεύω να μιλήσω για μαθηματικά! Απλώς την ρίζα του δύο την ξαναθυμήθηκα πριν μερικές μέρες, γιατί ανακάλυψα κάτι που εμένα μου φάνηκε πολύ παράξενο και που δεν το είχα αντιληφθεί όλα αυτά τα χρόνια! Βέβαια, η ρίζα του δύο είναι σημαδιακός αριθμός και μόνο γιατί ήταν ο πρώτος άρρητος που συναντήσαμε! Το γεγονός ότι ένας αριθμός είναι άρρητος (τα δεκαδικά του δηλαδή συνεχίζουν και συνεχίζουν και δεν σταματούν ποτέ) είναι από μόνο του παράξενο, αν και μετά από τόσα χρόνια μπορεί να μας φαίνεται σαν κάτι το φυσιολογικό ή και να το έχουμε ξεχάσει. Όμως υπάρχουν και κάμποσα άλλα περίεργα γύρω από αυτόν τον αριθμό. Ποιά ακριβώς; Ελάτε σε ένα ταξίδι που θα ξεκινήσει από την Βαβυλώνα, θα κάνει μία σύντομη στάση στην Ινδία, θα μείνει αρκετά στη Σχολή του Πυθαγόρα στον Κρότωνα και θα καταλήξει στο σήμερα και τις σύγχρονες εκτυπώσεις!

1. Από πότε ο άνθρωπος ξέρει την ρίζα του δύο; Όσο θαυμαστό κι’ αν είναι, ο υπολογισμός της ρίζας του δύο χάνεται στα βάθη των αιώνων! Η άποψη σήμερα είναι ότι Βαβυλώνιοι ήταν εκείνοι που πρώτοι τον υπολόγισαν με κάποια ακρίβεια! Η ανακάλυψη αυτή χρειάστηκε πολλά χρόνια ανασκαφές, αντιπαραβολή αντικειμένων, συσχετίσεις και φαντασία.

Πρώτα διαπιστώθηκε ότι οι Βαβυλώνιοι έγραφαν με μια γραφή “σφηνοειδή”. Την είπαν σφηνοειδή γιατί οι πήλινες πλάκες που ανακαλύπτονται στην περιοχή που άνθισε ο πολιτισμός τους, έχουν σημάδια σαν αγκάθια, μυτερά από την μία άκρη και πιό φαρδιά από την άλλη. Αυτό ήταν το πιό εύκολο για τους Βαβυλώνιους που έγραφαν πάνω σε πηλό. Χρησιμοποιούσαν κάτι σκληρό, μια μύτη από καλάμι ας πούμε και χάραζαν τον φρέσκο πηλό προτού ψηθεί. Όταν ο πηλός ψηνόταν έμενε μια πλάκα χαραγμένη και σκληρή που μπορούσε να κρατήσει το αρχείο ανέπαφο για πολλά χρόνια. Για να είμαστε ειλικρινείς, πολύ περισσότερα χρόνια απ’ ότι θα κρατήσουν τα αρχεία τους οι σύγχρονοι “σκληροί” δίσκοι!

Αφού κατάλαβαν οι αρχαιολόγοι τον τρόπο που έγραφαν οι Βαβυλώνιοι, με πολύ κόπο μπόρεσαν να διαβάσουν κάποια κείμενα που κατά βάση ήταν λογιστικά για το εμπόριο, αποστολές εμπορευμάτων, καταγραφές, χρεώσεις, αποθήκες και δασμοί. Το επόμενο βήμα ήταν να απομονώσουν και να αποκρυπτογραφήσουν τους αριθμούς.

Η ανάγνωση των αριθμών αποδείχτηκε ακόμη πιό δύσκολο έργο. Βλέπετε, οι Βαβυλώνιοι μέτραγαν στο εξηκονταδικό σύστημα, σε σύστημα δηλαδή που είχε βάση το 60, όχι το 10 (αυτό κι’ αν είναι παράξενο!)! Αφού κατέληξαν και σε αυτό και άρχισαν να καταλαβαίνουν και τους αριθμούς, οι αρχαιολόγοι πήγαν να αποκρυπτογραφήσουν μια περίεργη πήλινη πλάκα που είχαν βρει, καταχωρημένη σαν αντικείμενο YBC 7289 (Εικόνα 1).

Στην πλακέτα είναι χαραγμένο ένα τετράγωνο πλευράς τριάντα με τις δύο διαγωνίους του, η ρίζα του δύο και παράδειγμα υπολογισμού της διαγωνίου με την χρήση της ρίζας! Η ρίζα αναγράφεται ως 1,24,51,10 επάνω στην οριζόντια διαγώνιο. Για να την μετατρέψουμε στο δεκαδικό πρέπει να εκτελέσουμε την πράξη :

√2 = 1+(24/60)+(51/60²)+(10/60³) = 1,41421296 !!

Η ακρίβεια του υπολογισμού είναι 6 δεκαδικά ψηφία! ΕΞΙ ΔΕΚΑΔΙΚΑ ΨΗΦΙΑ! Σε μια πλάκα που χρονολογείται στο 1800 με 1600 π.Χ., είναι δηλαδή πολύ αρχαιότερη του πολέμου της Τροίας!!!

2. Πότε ανακαλύφθηκε ότι η ρίζα του δύο είναι άρρητος αριθμός; Στα χρόνια που ακολούθησαν η ρίζα του δύο θεωρείτο ρητός αριθμός. Και οι άνθρωποι προσπαθούσαν να τον εντοπίσουν. Οι Ινδοί μαθηματικοί για παράδειγμα θεωρούσαν ότι η ρίζα του δύο είναι ίση με το κλάσμα 577/408 που το κινητό μου λέει ότι ισούται με 1,41421568627! Και το χρησιμοποιούσαν από το 800 μέχρι το 200 π.Χ.. Παρότι είχαν περάσει κάπου χίλια χρόνια από την Βαβυλώνα, η ακρίβειά του είναι ελάχιστα καλύτερη από εκείνη των Βαβυλωνίων!.

Έτσι φτάνουμε στο τέλος του 6ου προ Χριστού αιώνα και στους Πυθαγόρειους!Από το τέλος του Έκτου αιώνα ο Πυθαγόρας είχε ιδρύσει την Σχολή του στον Κρότωνα της Ιταλίας. Το κίνημα που δημιούργησε δεν ήταν ακριβώς μαθηματικό με την σημερινή σημασία της λέξεως. Επρόκειτο για μία “σέχτα” Φιλοσοφικο – Θρησκευτικο -Πολιτική, που στηριζόταν στα Μαθηματικά! Βασική τους δοξασία ήταν ότι όλο το Σύμπαν είναι φτιαγμένο με βάση τα Μαθηματικά και ξεκίναγε από την ιδέα της τετρακτύος που είναι οι αριθμοί από ένα έως τέσσερα που θεωρούνταν ιεροί και είχαν συγκεκριμένη λειτουργία στην δημιουργία του κόσμου. Μάλιστα το ένα αντιπροσώπευε το υπέρτατο όν! Όλα τα πράγματα στον κόσμο αντιστοιχούσαν σε κάποιον ρητό αριθμό, δηλαδή σε έναν φυσικό αριθμό ή στον λόγο δύο φυσικών αριθμών! Έτσι το 577/408 των Ινδών, παραδείγματος χάριν, είναι ρητός αριθμός, αποδεκτός στους Πυθαγόρειους που γι’ αυτούς, άλλο είδος αριθμών δεν υπήρχε! Εμφανίζεται όμως ο Ίππασος (Εικόνα 2).

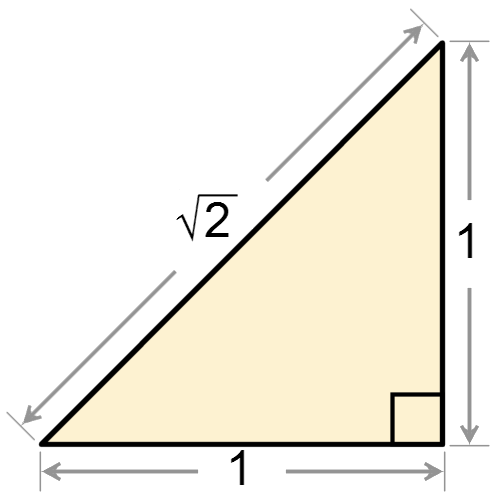
Ετούτος είναι γνωστός ως ο Μεταπόντιος ή Μεταποντίνος γιατί σύμφωνα με τον Αριστοτέλη είχε καταγωγή από το Μεταπόντιον, πόλη κοντά στον Κρότωνα. Ο Ίππασος έδρασε τα πρώτα 40 χρόνια του πέμπτου προ Χριστού αιώνα. Ήταν από τους πρώτους και καλύτερους μαθητές του Πυθαγόρα. Επειδή ήταν ιδιαίτερα καλός στα μαθηματικά ανέλαβε να οργανώσει και διευθύνει το Μαθηματικό Τμήμα της Σχολής. Ήταν φοβερά επίμονος και ευφυής. Δούλεψε πολύ πάνω στο Πυθαγόρειο θεώρημα και προσπάθησε άκαρπα να υπολογίσει τον ρητό αριθμό που αντιστοιχεί στην υποτείνουσα ενός ορθογωνίου τριγώνου με πλευρές μήκους ένα, την ρίζα του δύο, δηλαδή! Τελικά χρησιμοποιώντας την μέθοδο της “εις άτοπον απαγωγής”, που είναι δική του ανακάλυψη, κατάφερε να αποδείξει ότι η διαγώνιος αυτή δεν μπορεί να είναι ρητός αριθμός, δηλαδή κλάσμα φυσικών αριθμών. Εμφανίζεται λοιπόν για πρώτη φορά στον κόσμο ένα “νέο” είδος αριθμών, οι άρρητοι, που τα δεκαδικά τους ψηφία δεν σταματούν ποτέ, στον αιώνα τον άπαντα! (Σήμερα η ρίζα του δύο έχει υπολογιστεί με ακρίβεια δέκα ΤΡΙΣΕΚΑΤΟΜΜΥΡΙΩΝ ψηφίων, από τον Ron Watkins στις 28 Ιουνίου του 2016!! Ά τι κάνουν οι υπολογιστές!)

Η ανακάλυψη των αρρήτων αριθμών σήμαινε για τους Πυθαγόρειους την κατάρρευση της αρμονίας της φύσης, όπως την εννοούσαν εκείνοι. Βαρύ το χτύπημα! Δεν έφτανε όμως αυτό! Ο Ίππασος, σύμφωνα με τον Διογένη τον Λαέρτιο έγραψε σύγγραμα, τον “Μυστικόν Λόγον” για να επικοινωνήσει το εύρημά του στην ανθρωπότητα, καθώς πίστευε ότι ένα τόσο σημαντικό εύρημα δεν έπρεπε να κρατείται μυστικό!!

Οποία καταστροφή! Οι Πυθαγόρειοι μετά από αυτό, έπρεπε να διαλύσουν την Σχολή και να εξαφανιστούν! Όμως όχι, προσπάθησαν να “κουκουλώσουν” τα πράγματα. Έπνιξαν στην θάλασσα τον Ίππασο(!!!!) και προσπάθησαν να εξαφανίσουν τα ενοχοποιητικά στοιχεία χωρίς φαίνεται μεγάλη επιτυχία, καθώς μετά από μερικά χρόνια η Σχολή πράγματι διαλύθηκε.

Η απόδειξη του Ίππασου, εξαιρετικής ομορφιάς, είναι αυτή που μας μαθαίνουν όταν πρωτοσυναντούμε στα μαθηματικά τους άρρητους αριθμούς (αυτό για όσους βέβαια, κάτι θυμούνται ακόμη!).

Το τραγικό στην ιστορία αυτή είναι ότι η ρίζα του δύο σήμερα είναι γνωστή ως ο αριθμός του Πυθαγόρα (!) και όχι του Ίππασου!!!

3. Τί σχέση έχει η ρίζα του δύο με τις σύγχρονες εκτυπώσεις; Κάτι το απίθανο ανακάλυψα τώρα τελευταία! Ας ξεκινήσουμε παρατηρώντας τις διαστάσεις των χαρτιών εκτυπώσεως. Δεν χρειάζεται να εξετάσουμε όλες τις προδιαγραφές! Μπορούμε απλώς να δούμε τις προδιαγραφές των μεγεθών χαρτιού που είναι πιό γνωστά σε εμάς. Πάντως το ίδιο ισχύει ΣΕ ΟΛΕΣ ΤΙΣ ΠΡΟΔΙΑΓΡΑΦΕΣ ΤΩΝ ΧΑΡΤΙΩΝ ΕΚΤΥΠΩΣΕΩΣ ΚΑΙ ΣΕ ΟΛΟΝ ΤΟΝ ΚΟΣΜΟ! Ας δούμε λοιπόν τις διαστάσεις των χαρτιών εκτυπώσεως από Α0 έως Α6 και τον λόγο Ύψους / Πλάτος αφήνοντας τα υπόλοιπα μεγέθη της Α προδιαγραφής αλλά και όλα τα μεγέθη των υπολοίπων προδιαγραφών σε όσους θέλουν να επιβεβαιώσουν τον κανόνα (Εικόνα 3):

Μεγέθη χαρτιού	Πλάτος (χιλιοστά)	Ύψος (χιλιοστά)	Ύψος / Πλάτος (για το ίδιο μέγεθος)	Ύψος αυτού του χαρτιού / Πλάτος επομένου
Α0	841	1189	1189/841=1,4137	1189/594=2,001
Α1	594	841	841/594=1,4158	841/420=2,002
Α2	420	594	594/420=1,4142	594/297=2,000
Α3	297	420	420/297=1,4141	420/210=2,000
Α4	210	297	297/210=1,4142	297/148=2,007
Α5	148	210	210/148=1,4189	210/105=2,000
Α6	105	148	148/105=1,4095	….
………..	….	….	….	….

Παρατηρούμε τρία πράγματα :

Ι. το πλάτος του μεγαλύτερου χαρτιού είναι ίσο με το ύψος του αμέσως μικροτέρου

ΙΙ. ο λόγος ύψους προς πλάτος στο ίδιο χαρτί ισούται περίπου με την ρίζα του δύο και

ΙΙΙ. ο λόγος του ύψους του ενός χαρτιού προς το πλάτος του αμέσως μικροτέρου είναι εξαιρετικά κοντά στο δύο!!!!

Τυχαίο; – Ασφαλώς και όχι!! Το πρόβλημα που αντιμετωπίζεται στις εκτυπώσεις είναι ότι κάθε φορά που πρέπει να εκτυπώσουμε υπό κλίμακα, αυτό πρέπει να γίνεται γρήγορα και μεθοδικά. Αν για παράδειγμα έχουμε ετοιμάσει ένα έγγραφο για Α4 και τελικά, για να κάνουμε οικονομία αποφασίσουμε να τυπώσουμε 2 σελίδες σε μια όψη του Α4, τί κάνει ο υπολογιστής; Παρατηρώντας το πιό κάτω Σχήμα (Εικόνα 4):

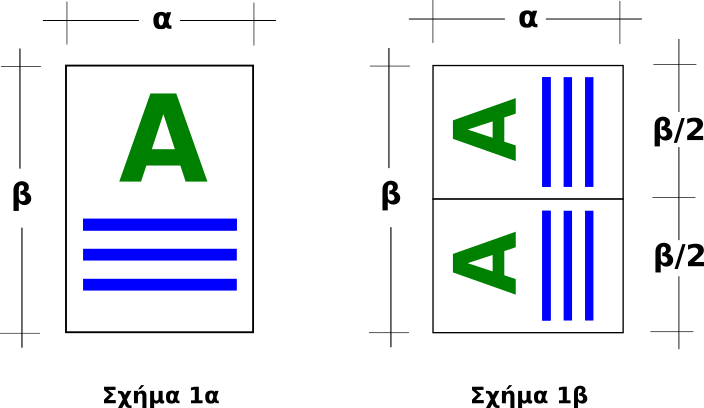
1ον. θα μικρύνει την σελίδα και θα μετατρέψει το πλάτος της αρχικής σελίδας από α σε β/2 για να χωρέσουν δύο σελίδες σε ένα Α4, το δε ύψος της αρχικής από β θα το μετατρέψει σε α. Να πως εξηγούνται οι παρατηρήσεις Ι και ΙΙΙ πάρα πάνω!

2ον. Θα στρέψει τις σελίδες που προκύπτουν κατά 90⁰ μοίρες αριστερά.

3ον. Για να μπορέσουν οι δύο νέες μικρές σελίδες να χωρέσουν στο χώρο της παλιάς χωρίς παραμόρφωση θα πρέπει να παραμείνει αναλλοίωτος ο λόγος Ύψους/Πλάτος της σελίδας! Δηλαδή πρέπει ο λόγος β/α της αρχικής να ισούται με τον λόγο α/(β/2) της τελικής! (Σας κορόιδεψα! Σας είπα ότι δεν θα έχει μαθηματικά!)

Με άλλα λόγια β/α = α/(β/2) και β²/2 = α² και (αναδιατάσσοντας) β²/α² = 2 και τέλος

β/α = √2 !!!!

Να λοιπόν πως προκύπτει η παρατήρηση ΙΙ παραπάνω και γιατί οι προδιαγραφές του χαρτιού προβλέπουν τον λόγο ύψους προς πλάτος της σελίδας να είναι περίπου ίσος με την ρίζα του δύο! Απλώς δεν θα μπορούσε να γίνει διαφορετικά!

Με αυτόν τον τρόπο ο υπολογιστής κάνει εκτυπώσεις υπό οποιαδήποτε κλίμακα γρήγορα και αποτελεσματικά χρησιμοποιώντας απλώς δύο αριθμούς, το 2 και την √2, μία ή περισσότερες συνεχόμενες φορές, για όσο χρειάζεται.

Συμπέρασμα : Οι προδιαγραφές του χαρτιού εκτυπώσεως έχουν αυτά τα περίεργα χαρακτηριστικά για ευκολία και ομοιομορφία στις αλλαγές κλίμακος εκτυπώσεως!

Και φτάσαμε στο τέλος του σημερινού ταξιδιού. Όσοι άντεξαν να φτάσουν μέχρι εδώ ελπίζω να το διασκέδασαν, ή έστω, να έμαθαν κάτι καινούργιο!

Δημήτρης Κατελούζος

13 Ιουνίου 2021